Оригинал: Linear Regression for Humans: Predicting the Future in Plain English
Перевод для канала Мы ж программист
Вы, возможно, уже делали линейную регрессию в голове:
- Чем больше кофе я выпью, тем будет труднее заснуть.
- Чем дольше идет дождь, тем зеленее выглядит трава.
- Чем старше я становлюсь, тем хуже себя чувствуют колени.
Линейная регрессия — это наука о построении наилучшей прямой линии на основе ваших данных, которая поможет вам понять взаимосвязи и сделать прогнозы. Это инструмент для определения общей взаимосвязи, даже если отдельные моменты не соответствуют ей в точности.
Конечно, в таких ситуациях есть и исключения. Не у всех есть проблемы с коленями, и воздействие кофеина на каждого человека неодинаково.
Но если бы вы опросили 500 человек и спросили их, сколько кофе они пьют и сколько времени им требуется, чтобы заснуть, вы бы получили точечную диаграмму, которая имеет тенденцию к увеличению. Вы могли бы провести прямую линию прямо посередине, и это могло бы выглядеть примерно так:
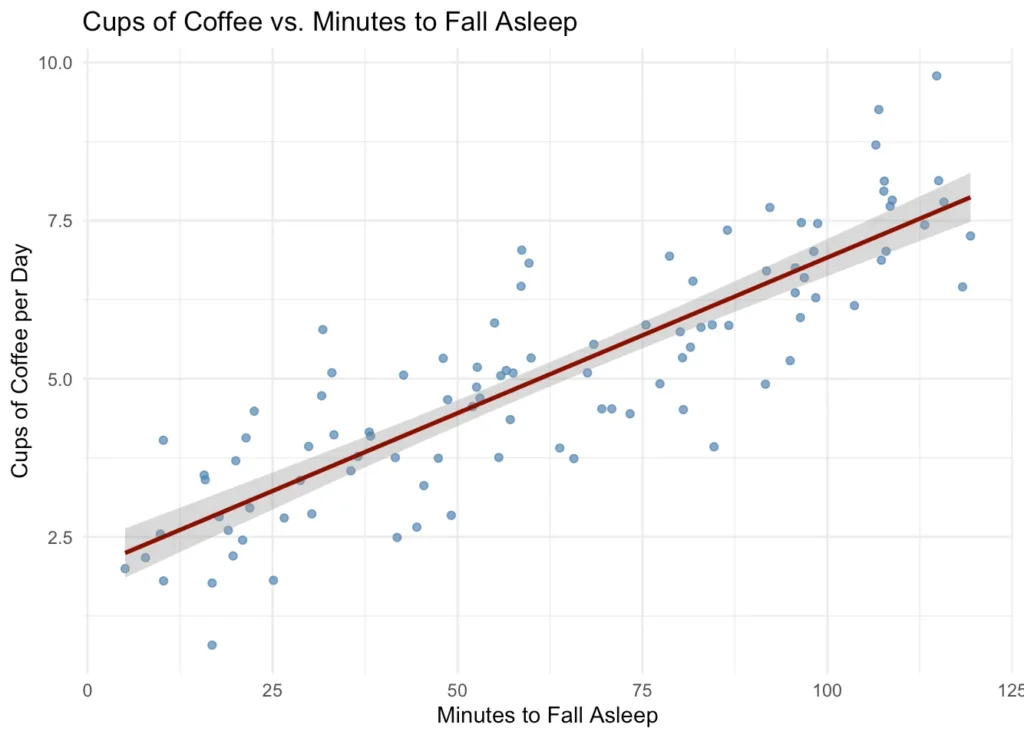
В реальной жизни много беспорядка. Некоторые высокие люди весят меньше, чем некоторые низкорослые. Некоторые учатся хуже, но получают более высокие оценки.
Но если вы оглянетесь назад, то увидите тенденцию:
- Более высокие люди, как правило, весят больше.
- Более интенсивная учеба, как правило, приводит к более высоким баллам.
В этой статье мы рассмотрим линейную регрессию простым языком, без использования кода или сложной математики. Просто примеры размером с пиццу, которые вы сможете понять.
Как нарисована линия?
Вот важная часть из урока статистики: «линия наилучшего соответствия» выбирается путем минимизации ошибок. Этот метод называется обычным методом наименьших квадратов (МНК, OLS). Думайте об этом как о линии, которая в целом является наименее неправильной. Другими словами, линия выбирается таким образом, чтобы расстояние между фактическими точками и линией было в среднем как можно меньше.
Представьте, что каждая точка на приведенном выше графике привязана к линии тонкой резинкой. Если линия расположена далеко, лента натягивается туго. OLS — это как бы регулировка линии до тех пор, пока общее растяжение по всем полосам не станет как можно меньше.
Простой пример регрессии: размер и цена пиццы
Вы просматриваете меню своей любимой пиццерии. Вы замечаете, что пицца большего размера стоит дороже. Итак, вы собираете данные.
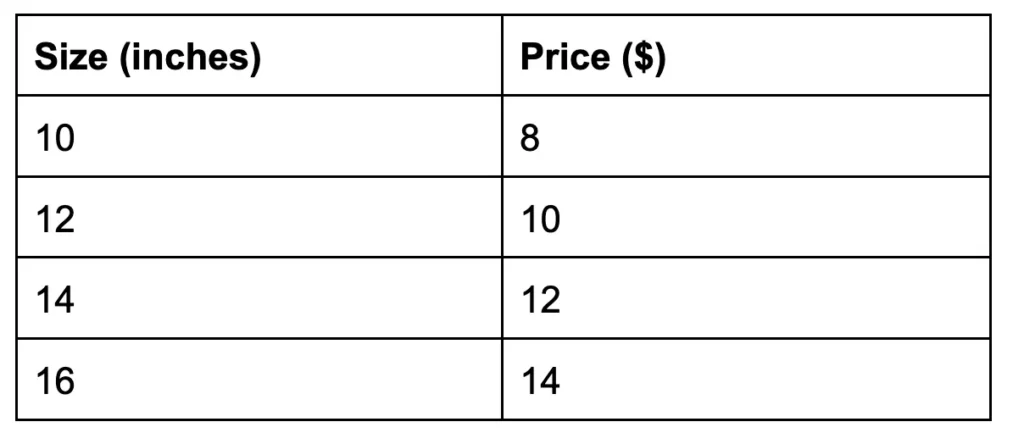
Вы можете взять миллиметровку и нанести эти точки на график, как вы делали на уроке алгебры, и это подтвердит, что существует зависимость между размером пиццы и ее стоимостью.
Линейная регрессия — это математика, стоящая за этой линией.
Так что, если кто-нибудь спросит: «Сколько будет стоить 15-дюймовая пицца?», вы можете посмотреть на строку и ответить: «Вероятно, около 13 долларов». И будьте осторожны, это все равно прогноз, а не точная цифра. Прогнозы могут быть неверными.
- В статистике линейная регрессия часто используется для объяснения взаимосвязей («насколько сильно меняется x при изменении y?»).
- В машинном обучении линейная регрессия обычно используется для прогнозирования («учитывая эти входные данные, какой результат мы должны ожидать?»).
На самом деле, вы не смогли бы построить модель машинного обучения для определения цены на пиццу, но обе они используют одну и ту же математическую основу: поиск линии, которая минимизирует ошибку.
Однако, вот еще что: мы не можем предполагать, что все отношения линейны. Если зависимость является кривой (например, возраст и зарплата часто сначала увеличиваются, а затем выравниваются), прямая линия не сможет ее отразить, и модель линейной регрессии не сработает. Приведем пример ниже: линия не подходит.
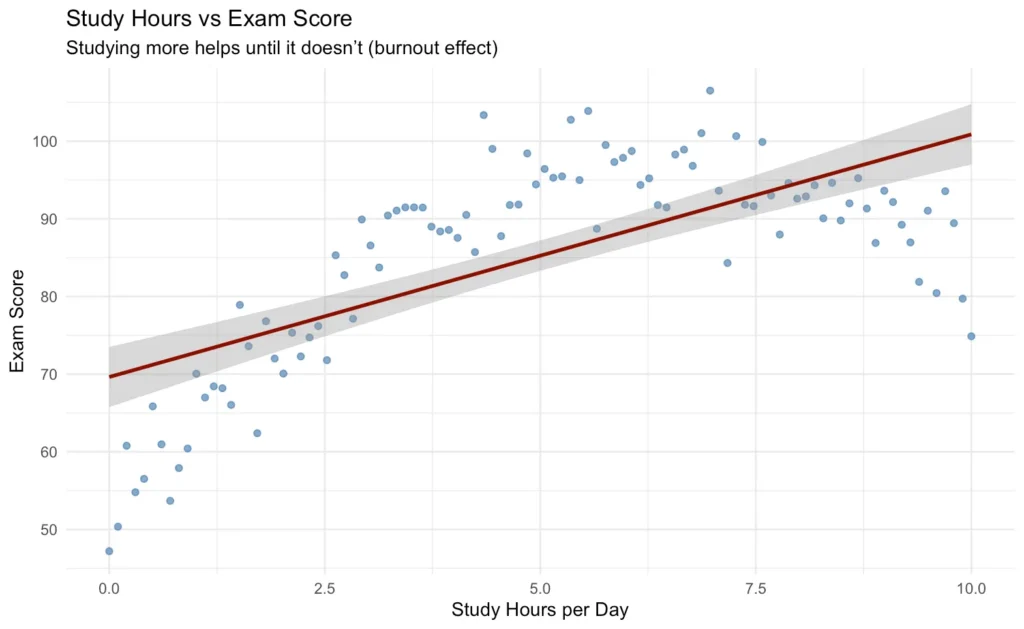
Что говорит нам линейная регрессия?
Итак, если вы работаете в какой-либо области, где люди задаются вопросом, насколько увеличатся продажи или сколько потратит клиент, линейная регрессия обычно является первым методом, который вы пробуете в качестве специалиста по обработке данных. Он предсказывает постоянный результат.
И его легко объяснить людям, не имеющим отношения к технике:
Мы использовали прошлые данные, чтобы провести черту. Эта линия помогает нам предсказывать будущее.
Помимо составления прогнозов, линейная регрессия может рассказать вам:
- Направление взаимосвязи: Приводит ли увеличение x (размера) к увеличению y (цены)?
- Сила взаимосвязи: четкая ли линия или точки разбросаны повсюду?
- Важность: Какая переменная лучше всего помогает предсказать результат?
Модель линейной регрессии также даст вам некоторые дополнительные технические результаты:
- R² (R-квадрат): Насколько сильно отклонение от того, что вы прогнозируете, объясняется линией. Чем больше R², тем лучше соответствие.
- p-значения: является ли переменная статистически полезной или просто шумом.
- Коэффициенты (β): веса, применяемые к каждой переменной, которые показывают, насколько они важны для прогнозирования.
Но в этом посте мы не будем вдаваться в подробности о показателях модели. Далее давайте рассмотрим уравнение линейной регрессии. Не волнуйтесь, я объясню каждую часть.
Ингридиенты линейной регрессии
Вот классическое статистическое уравнение линейной регрессии:
ŷ = β₀ + β₁x₁ + ε
Это может выглядеть немного страшнее, чем уравнение формы наклона-пересечения из урока алгебры y = mx + b, но, по сути, оно говорит о том же, только с надлежащей статистической нотацией.
Вам не нужно запоминать какие-либо уравнения или уметь что-либо вычислять вручную, но это помогает понять, что происходит за кулисами.
Итак, давайте разберем это подробнее:
- ŷ — это ваше прогнозируемое значение, которое вы пытаетесь оценить (например, цена пиццы). Мы называем это зависимой переменной или «шапкой y» (англ. “y hat”).
- x — это ваши входные данные, которые вы используете для прогнозирования (размер пиццы). Мы можем использовать более одной переменной для прогнозирования ŷ, и в этом случае мы добавим в уравнение β₂x₂ и так далее. В примере с пиццей вы также можете добавить высококачественные начинки, уровень содержания сыра и тип коржа в качестве входных переменных для прогнозирования цены. Мы называем их информативные признаки (informative features) или независимые переменные (independent variables).
- β₁ — это наклон, то есть величина, на которую изменяется ŷ при каждом увеличении x на единицу (например, на сколько увеличивается цена за каждый дополнительный дюйм). Мы также называем это веса (weights) или коэффициенты (coefficients), применяемые к каждой переменной x.
- β₀ — это пересечение — прогнозируемое значение, когда x = 0 (часто не имеет смысла, но это часть математики). Мы также называем это «бета-нулем». Это устанавливает начальную точку линии до того, как другие переменные (наклоны) изменят ее вверх или вниз.
- ε — это ошибка, «шум» или случайность, которую мы не можем объяснить. В машинном обучении мы предпочитаем считать, что это усредняется, но это важно в статистике.
Линейная зависимость может быть слабой (много шума) или жесткой (меньше шума). Рассмотрим пример ниже:
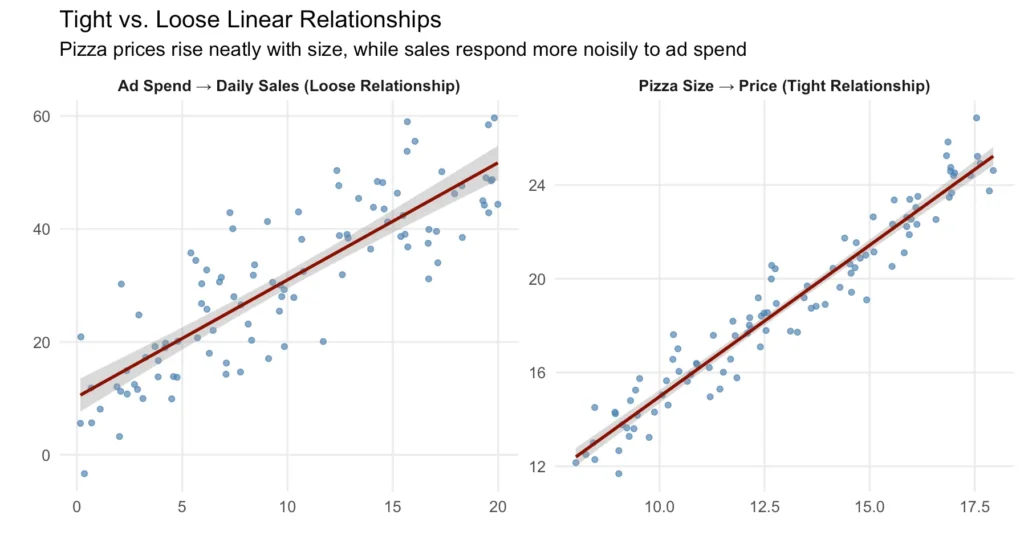
Однако будьте осторожны, если две вещи движутся вместе, это не значит, что одна вызывает другую. Большее количество пожарных на пожаре не приводит к большему ущербу; размер пожара влияет и на то, и на другое.
Мы также должны быть осторожны, чтобы не добавить в нашу модель слишком много информативных признаков, которые сделают ее запутанной и не позволят делать правильные прогнозы на основе невидимых данных. Переменные, которые измеряют почти одно и то же (например, «размер пиццы» и «количество ломтиков»), могут запутать модель. Это называется мультиколлинеарностью.
Вам также нужно будет решить, относятся ли «выбросы» к вашему набору данных или нет. Существует множество причин для появления «выбросов»; иногда их можно оставить, но иногда это не так.
И если вы решите, что хотите добавить больше данных, вы можете удлинить список (найти больше строк или образцов) или расширить его (добавить больше признаков — features).
- Глубокий (больше строк/наблюдений): лучше для повышения надежности вашей модели и уменьшения количества помех.
- Широкий (больше столбцов/признаков): лучше для того, чтобы сделать вашу модель более понятной или отразить большую сложность.
Создание дополнительных признаков с использованием существующих данных называется обогащением признаков или разработкой признаков. Например, если в вашем наборе данных есть размер пиццы и количество ломтиков, вы можете создать новую функцию, например, цену за кусочек. Это и есть разработка признаков.
Но если этого будет слишком много, наша модель может начать запоминать особенности обучающих данных вместо того, чтобы изучать общую закономерность. Создание новых функций не исправит некачественные данные. Если исходные данные зашумлены или искажены, инженерные функции только усилят шум. (Мусор на входе, мусор на выходе.)
Классификация vs. Линейная регрессия: в чем разница?
Представьте, что вы устроились на работу специалистом по обработке данных в свою любимую пиццерию. К вам приходят два разных менеджера с двумя разными вопросами. Один менеджер спрашивает:
Не могли бы вы сказать мне, что клиент закажет: пепперони или сыр?
Это проблема классификации.
Вы присваиваете ярлык, в данном случае «пепперони» или «сыр». Вы предсказываете категории, например:
- Спам или не спам
- Высокий риск или низкий риск
Задача модели — предсказать класс на основе определенных переменных x, которыми могут быть день недели, время суток, возраст, местоположение и т.д. Целью может быть бинарная классификация (два варианта) или многоклассовая (много вариантов). Суть в том, что вы прогнозируете категории, а не непрерывные цифры по шкале.
Позже в тот же день другой ваш менеджер спрашивает:
Можете ли вы оценить, сколько клиент потратит на свой заказ?
Это проблема регрессии. Вы прогнозируете цифру, например, $18,75.
Регрессионные модели используются, когда ваш результат является непрерывным (он может принимать различные значения), например:
- Как далеко?
- Как долго?
- Какой счет?
Как и классификация, прогнозирование с помощью линейной регрессии также основано на определенных переменных x, которыми могут быть день недели, время суток, заказ напитков, доставка или самовывоз, местоположение и т.д.
Классификация позволяет определить, какие именно напитки. Регрессия позволяет определить, в каком количестве.
Чем это отличается от временных рядов?
Если вы читали о временных рядах, то знаете, что одна вещь священна: порядок данных.
Во временных рядах сегодняшний день зависит от вчерашнего. Вы распределяете данные по временному порядку, а не случайным образом.
Но при линейной регрессии все наоборот:
- Каждая строка должна быть независимой.
- Случайное разделение на тренинги и тесты допустимо, если будущее не вытекает из прошлого.
- Автокорреляция (точки зависят друг от друга) нарушает допущения регрессии.
Таким образом, в то время как модели временных рядов предсказывают, что произойдет дальше, регрессионные модели отвечают на то, что наиболее важно прямо сейчас.
Объяснение vs. Предсказание
Теперь, когда вы знаете, что такое линейная регрессия, я хочу упомянуть о нюансе, который легко упустить из виду:
Регрессия может быть двух типов. Она может быть объяснительной или прогностической, но не всегда и то, и другое одновременно.
- Объяснительная регрессия может гласить: «Каждый дополнительный год опыта работы увеличивает зарплату на 5000 долларов, а все остальное остается неизменным». Это отлично подходит для понимания взаимоотношений.
- Прогнозирующая регрессия может сказать: «Исходя из размера, характеристик и местоположения, этот дом должен продаваться за 350 000 долларов». Она направлена на то, чтобы правильно рассчитать цифру, а не рассказать историю.
Оба этих метода могут быть использованы в бизнесе. Вы можете построить модель линейной регрессии, которая либо объясняет, либо предсказывает.
В обоих случаях используется одна и та же математика, но основное внимание уделяется различиям: в одном случае речь идет о понимании взаимосвязей, а в другом — о точных предположениях.
Заключение
Линейная регрессия — от оценки цен на пиццу до прогнозирования выручки — является одним из наиболее широко используемых инструментов в области обработки данных. Часто это первая модель, к которой вы обращаетесь, когда кто-то спрашивает «сколько стоит?»
Вот несколько важных моментов, которые следует учитывать при объяснении линейной регрессии:
- Линейная регрессия находит линию, которая минимизирует ошибку во всех ваших данных; линию, которая в целом является наименее ошибочной.
- Она предсказывает непрерывные значения (например, цену или доход), а не категории.
- Коэффициенты (β) показывают, насколько каждая переменная влияет на прогноз.
- R² показывает, насколько хорошо подходит линия, в то время как p-значения помогают определить, какие функции действительно важны.
- Корреляция не является причинно-следственной связью.
- Выбросы и мультиколлинеарность могут исказить вашу модель, поэтому важна очистка данных и выбор признаков.
- Добавление дополнительных признаков (feature engineering) может помочь, но их чрезмерное количество может привести к переобучению.
- Регрессия может быть объяснительной («каждый год опыта работы увеличивает зарплату на $5k») или прогнозирующей («этот дом можно продать за $350k»), но редко бывает и тем и другим одновременно.
Линейная регрессия не даст вам точных ответов, но она даст вам четкую, понятную отправную точку. Надеюсь, теперь вы будете более уверены в себе, когда в следующий раз кто-нибудь спросит: «Сколько это будет стоить?»
